Etapa 1: 01.10.2007 - 15.12.2007
Raport anual de activitate - 2007
S I N T E Z A
Obiectivul 1 : Model bazat pe teoria gauge cuantica a gravitatiei
1.1.Definirea integralei actiunii
S-a construit unui model pentru câmpurile gauge (clasice si cuantice) bazat pe teoria gauge cuantica a gravitatiei. Grupul de simetrie gauge gravitational G folosit consta din transformarile ) infinitezimale [1, 10]:
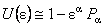 , , 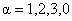 , (1) , (1)
unde 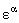 sunt parametrii infinitezimali ai grupului si sunt parametrii infinitezimali ai grupului si 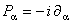 sunt generatorii acestui grup. Relatiile de comutare dintre acesti generatori sunt: sunt generatorii acestui grup. Relatiile de comutare dintre acesti generatori sunt:
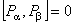 . (2) . (2)
S-a introdus apoi 1-forma de câmp cu valori în algebra Lie a grupului G , prin relatia :
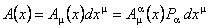 , , 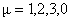 , (3) , (3)
unde 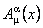 sunt potentialele gauge gravitationale. Cu ajutorul acestora, s-a construit derivata gauge covarianta: sunt potentialele gauge gravitationale. Cu ajutorul acestora, s-a construit derivata gauge covarianta:
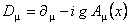 , (4) , (4)
unde g noteaza constanta de cuplaj gauge pentru interactiunile gravitationale.
Este mai convenabil sa lucram cu alte potentiale gauge, echivalente:
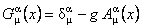 . (5) . (5)
Presupunem ca aceste noi potentiale admit inversele 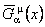 , conform conditiilor: , conform conditiilor:
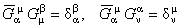 . (6) . (6)
Construim apoi 2-forma de curbura 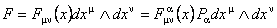 , asociata acestor potentiale si luând valori în algebra Lie a grupului G , unde , asociata acestor potentiale si luând valori în algebra Lie a grupului G , unde
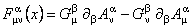 . (7) . (7)
Pentru a face legatura cu teoria relativitatii generale, construim apoi tensorul metric pe spatiul grupului gauge gravitational:
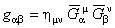 , (8.a) , (8.a)
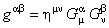 , (8.b) , (8.b)
unde 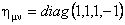 este tensorul metric al spatiului-timp Minkowski M si este tensorul metric al spatiului-timp Minkowski M si 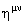 inversul sau. inversul sau.
S-a definit apoi integrala actiunii pentru câmpul gravitational sub forma [1]:
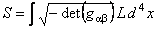 , (9) , (9)
unde 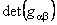 noteaza determinantul tensorului metric noteaza determinantul tensorului metric 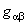 si L este densitatea de Lagrangian a câmpului gravitational. Deoarece am urmarit sa introducem in model constanta cosmologica si L este densitatea de Lagrangian a câmpului gravitational. Deoarece am urmarit sa introducem in model constanta cosmologica 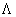 , s-a ales L de forma [1]: , s-a ales L de forma [1]:
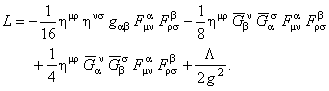 (10) (10)
Impunând conditia de anulare a variatiei actiunii S sub forma 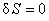 , in raport cu potentialele gauge , in raport cu potentialele gauge 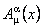 , s-au obtinut ecuatiile de câmp generale: , s-au obtinut ecuatiile de câmp generale:
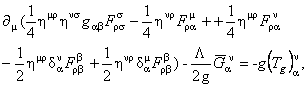 (11) (11)
unde 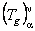 este tensorul energie-impuls gravitational considerat ca sursa a cestui câmp [3, 10]. Expresia acestui tensor s-a obtinut cu ajutorul unui program de calcul elaborat de noi, bazat pe sistemul MAPLE. S-a obtinut apoi o solutie pentru ecuatiile de câmp (11) considerând cazul când potentialele gauge au simetrie sferica [1, 4]: este tensorul energie-impuls gravitational considerat ca sursa a cestui câmp [3, 10]. Expresia acestui tensor s-a obtinut cu ajutorul unui program de calcul elaborat de noi, bazat pe sistemul MAPLE. S-a obtinut apoi o solutie pentru ecuatiile de câmp (11) considerând cazul când potentialele gauge au simetrie sferica [1, 4]:
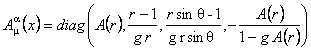 , (12) , (12)
unde A ( r ) este o functie numai de coordonata radiala r .
1.2. Calculul tensorului energie-impuls si obtinerea ecuatiilor de câmp
Folosind programul de calcul MAPLE [6, 8], s-au obtinut componentele tensorului 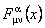 , ale metricii , ale metricii 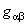 si si 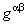 , precum si ale tensorului energie-impuls , precum si ale tensorului energie-impuls 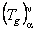 al câmpului gravitational. Prezentam aici câteva dintre componentele ne-nule, mai simple, ale lui al câmpului gravitational. Prezentam aici câteva dintre componentele ne-nule, mai simple, ale lui 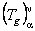 : :
 , (13) , (13)
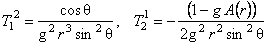 , ,
unde 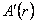 noteaza derivata functiei necunoscute A ( r ) in raport cu variabila r . noteaza derivata functiei necunoscute A ( r ) in raport cu variabila r .
Folosind aceste expresii s-au obtinut urmatoarele ecuatii de câmp [1]:
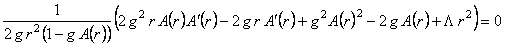 , (14) , (14)
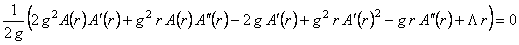 , (15) , (15)
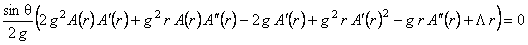  (16) (16)
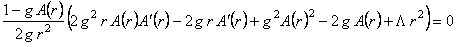 , (17) , (17)
unde 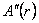 este derivata de ordinul al doilea în raport cu r a functiei este derivata de ordinul al doilea în raport cu r a functiei 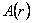 . .
1.3. Construirea unei solutii continând constanta cosmologica
Ecuatiile (14) – (17) sunt echivalente daca 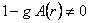 , astfel ca avem numai o singura ecuatie independenta pentru o singura functie necunoscuta , astfel ca avem numai o singura ecuatie independenta pentru o singura functie necunoscuta 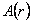 . Facând apoi notatia . Facând apoi notatia 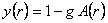 , din ecuatia (14) obtinem: , din ecuatia (14) obtinem:
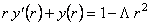 , (18) , (18)
cu solutia
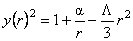 , (19) , (19)
unde 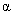 este o constanta arbitrara de integrare. Atunci, este o constanta arbitrara de integrare. Atunci,
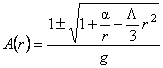 , (20) , (20)
si alegând 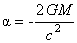 , unde M este masa sursei punctiforme a câmpului gravitational descris de , unde M este masa sursei punctiforme a câmpului gravitational descris de 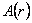 , din relatia (8.a) obtinem metrica Schwarzschild-de-Sitter al carei element de linie este: , din relatia (8.a) obtinem metrica Schwarzschild-de-Sitter al carei element de linie este:
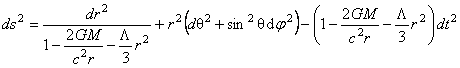 (21) (21)
Subliniem ca acest element de linie este definit pe spatiul grupului gauge gravitational G , iar spatiul-timp baza M ramâne de tip Minkowski (plat).
Concluzia importanta care rezulta din evaluarile de mai sus este ca putem trata gravitatia ca o interactiune fizica într-un spatiu-timp plat (fara curbura). Câmpul gravitational se descrie prin potentialele gauge 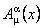 , iar metrica se construieste pe spatiul grupului gauge gravitational G si nu influenteaza spatiul-timp. Ca urmare, este mai usor sa obtinem modele cuantice pentru câmpul gravitational si, în general, pentru câmpurile gauge, folosind metoda integralei functionale [7], dat fiind ca spatiul-timp este plat. , iar metrica se construieste pe spatiul grupului gauge gravitational G si nu influenteaza spatiul-timp. Ca urmare, este mai usor sa obtinem modele cuantice pentru câmpul gravitational si, în general, pentru câmpurile gauge, folosind metoda integralei functionale [7], dat fiind ca spatiul-timp este plat.
Obiectivul 2 : Definirea produsului star dintre câmpurile pe spatii-timp necomutatve
2.1. Construirea unei derivate gauge-covarianta
S-a considerat un spatiu-timp necomutativ pentru descrierea teoriilor gauge. Aceasta înseamna ca se folosesc coordonate 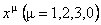 care satisfac relatiile de comutare: care satisfac relatiile de comutare:
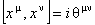 , (22) , (22)
unde 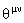 este o matrice constanta antisimetrica. În acest caz, trebuie sa înlocuim produsul obisnuit este o matrice constanta antisimetrica. În acest caz, trebuie sa înlocuim produsul obisnuit 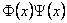 dintre doi operatori de câmp, prin produsul star „* „ conform definitiei: dintre doi operatori de câmp, prin produsul star „* „ conform definitiei:
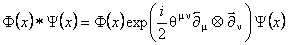 . (23) . (23)
Modelele necomutative bazate pe acest produs au neajunsul ca nu sunt Lorentz-invariante, în sensul ca relatia (22) nu este invarianta fata de transformarile Lorentz. Totusi, ele sunt invariante fata de algebra Poincaré deformata cu un operator (twist) abelian:
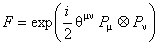 , (24) , (24)
unde 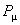 sunt generatorii translatiilor spatio-temporale definiti mai sus. Operatorul F induce in spatiul reprezentarilor algebrei Poincaré un produs deformat : sunt generatorii translatiilor spatio-temporale definiti mai sus. Operatorul F induce in spatiul reprezentarilor algebrei Poincaré un produs deformat :
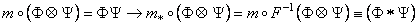 , (25) , (25)
care este tocmai produsul star „* „ din (23).
Atunci când operatorul twist F este ales ca în (24), produsul „* „ este fixat pentru totdeauna si deci el nu sufera vre-o modificare fata de transformarile unui grup gauge intern. Ca urmare, apar difcultati atunci când încercam sa deformam transformarile gauge interne cu acelasi operator twist (24). Este deci necesar sa gasim un principiu general de simetrie pe baza caruia sa putem construi teorii gauge necomutative si gravitationale lipsite de contradictii interne. Vom descrie în continuare rezultatele noastre privind un astfel de principiu [2].
Presupunem ca g este o algebra Lie de simetrie interna (de ex. asociata grupului gauge G ), ai carei generatori infinitezimali 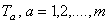 satisfac relatiile de comutare: satisfac relatiile de comutare:
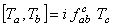 , , 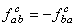 . (26) . (26)
unde 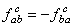 sunt constantele de structura . Daca presupunem apoi ca g este o algebra de simetrie locala (gauge), atunci o transformare gauge este data de operatorul: sunt constantele de structura . Daca presupunem apoi ca g este o algebra de simetrie locala (gauge), atunci o transformare gauge este data de operatorul:
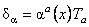 . (27) . (27)
Introducem, ca de obicei, câmpurile gauge , cu valori în algebra Lie, prin relatia:
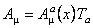 . (28) . (28)
Cu ajutorul lor construim derivate gauge-covarianta:
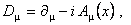 (29) (29)
care are proprietatea ca 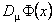 se transforma covariant pentru orice câmp se transforma covariant pentru orice câmp 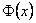 : :
 . (30) . (30)
În cazul când dorim sa avem un model care include simultan simetriile gauge interna g si externa P (Poincar é), trebuie sa folosim algebra Hopf  a produsului semi-direct dintre cele doua algebre. Atunci, derivata gauge covarianta trebuie scrisa sub forma: a produsului semi-direct dintre cele doua algebre. Atunci, derivata gauge covarianta trebuie scrisa sub forma:
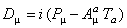 , (31) , (31)
unde 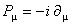 . .
În lucrarea [9] s-a aratat ca folosirea unui operator twist abelian pentru a deforma algebra Hopf  nu este compatibila cu conceptul de transformare gauge. Acest lucru se datoreste faptului ca derivata obisnuita nu este compatibila cu conceptul de transformare gauge. Acest lucru se datoreste faptului ca derivata obisnuita 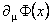 a unui câmp nu este gauge invarianta (nu se transforma ca si câmpul însusi). Însa, tinând seama de proprietatea (30), în lucrarea noastra [2] am definit un operator twist ne-abelian T folosind derivate gauge covarianta: a unui câmp nu este gauge invarianta (nu se transforma ca si câmpul însusi). Însa, tinând seama de proprietatea (30), în lucrarea noastra [2] am definit un operator twist ne-abelian T folosind derivate gauge covarianta:
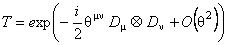 . (32) . (32)
Corespunzator, am definit un nou produs star  deformat, prin: deformat, prin:
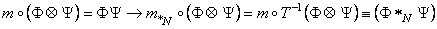 . (33) . (33)
• Verificarea proprietatilor produsului star
In general, acest nou produs star nu este asociativ, astfel încât trebuie sa-i acordam o deosebita atentie atunci când lucram cu el. Studiul operatorilor twist folosind derivata gauge covarianta ramâne o problema deschisa pentru noi cercetari. Totusi, pentru anumite clase de reprezentari ale algebrei Hopf  proprietatea de asociativitate este îndeplinita, asa cum aratam în continuare. proprietatea de asociativitate este îndeplinita, asa cum aratam în continuare.
Folosind algebra Hopf  drept algebra de simetrie pentru teoria gauge necomutativa, trebuie sa introducem pentru ea un co-produs drept algebra de simetrie pentru teoria gauge necomutativa, trebuie sa introducem pentru ea un co-produs  , un element unitate 1 si o co-unitate , un element unitate 1 si o co-unitate 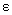 cu proprietatile: cu proprietatile:
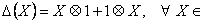  , (34) , (34)
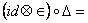 1 = 1 = 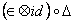 . (35) . (35)
Operatorul twist T trebuie sa satisfaca conditiile:
 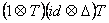 , (36) , (36)
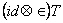 = = 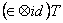 . (37) . (37)
In lucrarile noastre am verificat conditia (34) si am stabilit ca ea este îndeplinita numai pentru acele reprezentari ale algebrei  care satisfac constrângerile: care satisfac constrângerile:
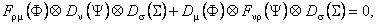 (38) (38)
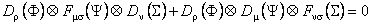 , (39) , (39)
unde 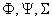 sunt câmpuri arbitrare care apartin spatiului de reprezentare. sunt câmpuri arbitrare care apartin spatiului de reprezentare.
Concluzia care rezulta din cercetarile noastre este ca simetria Poincaré externa si simetria gauge interna nu pot fi unificate într-un operator twist comun [2]. Acest lucru ar putea fi o consecinta a teoremei Coleman-Mandula, dar nu în întregime, deoarece aceasta teorema se refera la grupurile de simetrie globale. Este totusi posibil ca situatia sa se inverseze, având în vedere ca supersimetria include simetriile interne.
• Exemplu de model necomutativ bazat pe aplicatia Seiberg-Witten
Folosind rezultatele proprii anterioare, am obtinut corectii de necomutativitate pentru metrica (21), presupunând 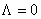 . Pentru aceasta, am folosit aplicatia Seiberg-Witten [11], obtinând urmatoarele expresii pentru componentele metricii pâna la ordinul al doilea în parametrul . Pentru aceasta, am folosit aplicatia Seiberg-Witten [11], obtinând urmatoarele expresii pentru componentele metricii pâna la ordinul al doilea în parametrul 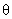 : :
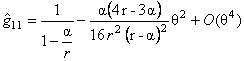 , (40) , (40)
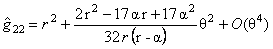 , (41) , (41)
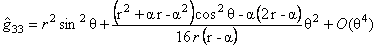 , (42) , (42)
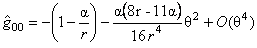 . (43) . (43)
unde s-a ales 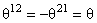 si restul componentelor lui si restul componentelor lui 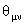 egale cu zero. egale cu zero.
Se observa ca în aceste expresii apar corectii de necomutativitate numai în ordinul al doilea în parametrul  . .
Având aceste corectii, se pot studia proprietatile termodinamice ale unui black hole. De asemenea, sunt posibile generalizari la alte metrici. Aceste aspecte vor fi abordate în etapele urmatoare ale proiectului.
Bibliografie
A. Lucrari proprii:
în reviste indexate ISI
- G. Zet , C. Popa , D. Partenie: Schwarzschild-de-Sitter Solution in Quantum Gauge Theory of Gravity, Commun. Theor. Phys. (Beijing, China), Vol. 47 (2007) pp. 843-846 (pdf)
- M. Chaichian, A. Tureanu, G. Zet : Twist as a symmetry principle and noncommutative gauge theory formulation, Phys. Lett. B651 (2007) pp. 319-323 (pdf)
în reviste indexate în baze de date internationale
- B. Ciobanu , I. Radinschi: Modeling the Energy Distributions of a Dilaton-Maxwell Gravity; va apare în Romanian Journal of Physics Vol. 53 , nr. 1-2 (2008) pp. 29-34 (pdf)
- G. Zet , C. Popa : Spherical gauge gravitation field and spontaneous symmetry breaking, 8-th International Balkan Workshop on Applied Physics, July 5-7, 2007, Constanta; acceptata pentru publicare în Romanian Journal of Physics 2008 (pdf)
- M. Chaichian, M. Setare, A. Tureanu, G. Zet : Noncommutative corrections for spherically symmetric gravitational fields, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- G. Zet , V. Manta , C. Popa : Analytical program for gauge models, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- V. Chiritoiu , G. Zet , S. Babeti: Quantization of gauge fields on de-Sitter group by functional integral method, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- S. Arustei , V. Manta : Quantum Computation Language Implementation of the Berstein-Vazirani Algorithm, 9-th International Symposium on Automatic Control and Computer Science, Iasi, November 16-17, 2007, Proceedings Ed. Politehnium, 2007, p. 179-182, ISSN 1843-7257; acceptata pentru publicare în Buletinul Institutului Politehnic Iasi, fasc. 1-4 Automatica si calculatoare, 2007 (pdf)
B. Lucrari ale altor autori:
- M. Chaichian, A Tureanu: Twist Symmetry and Gauge Invariance, Phys. Lett. B637 (2006) pp. 199-202
- N. Wu: Renormalizable Quantum Gauge Theory of Gravity, Commun. Theor. Phys. (Beijing, China), Vol. 38 (2002) pp. 151-156
- N. Seiberg, E. Witten: String Theory and Noncommutativity Geometry, JHEP 9909 (1999) 032
Sinteza etapei 1 in format PDF |