Stage 1
01.10.2007 - 15.12.2007
Objective 1: Model based on the quantum gauge theory of gravitation
1.1. The definition of the action integral
We construct a model for the gauge fields (classical and quantum) based on the quantum gauge theory of gravitation.
The gauge gravitational group G of symmetry has the infinitesimal transformations of the form [1, 10]:
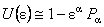 , , 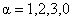 , (1) , (1)
where 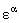 are the infinitesimal parameters of the group and are the infinitesimal parameters of the group and 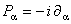 are the generators of gauge group G . The commutation relations of these generators are: are the generators of gauge group G . The commutation relations of these generators are:
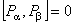 . (2) . (2)
As usually, we introduce the 1-form of the gauge gravitational field with values into the Lie algebra of the group G :
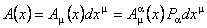 , , 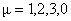 (3) (3)
where 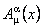 are the gravitational gauge potentials. Then, a gauge covariant derivative is defined as are the gravitational gauge potentials. Then, a gauge covariant derivative is defined as
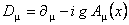 . (4) where g denotes the gauge coupling constant of the gravitational interactions. . (4) where g denotes the gauge coupling constant of the gravitational interactions.
It is more convenient to introduce new equivalent gauge potentials
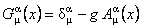 . (5) . (5)
We suppose that these new potentials admit the inverses 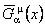 with the usual properties: with the usual properties:
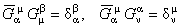 . (6) . (6)
Then, we construct the 2-form of curvature 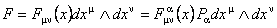 associated to these potentials, with values in the Lie algebra of G , having the components: associated to these potentials, with values in the Lie algebra of G , having the components:
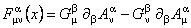 . (7) . (7)
In order to make comparison with General Relativity, we define a metric tensor on the gravitational gauge group space by:
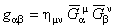 , (8.a) , (8.a)
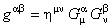 . (8.b) . (8.b)
where 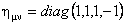 is the metric tensor of the Minkowski space-time M, and is the metric tensor of the Minkowski space-time M, and 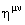 denotes its inverse. denotes its inverse.
We define the integral of action for the gravitational gauge potentials under the form:
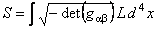 , (9) , (9)
where 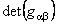 is the determinant of the metric tensor is the determinant of the metric tensor 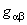 , and L is the Lagrangian density of the gravitational field. Because we want to introduce the cosmological constant , and L is the Lagrangian density of the gravitational field. Because we want to introduce the cosmological constant 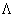 in our model, we chose L of the form: in our model, we chose L of the form:
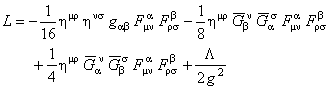 (10) (10)
Taking 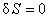 with respect to gravitational gauge potentials with respect to gravitational gauge potentials 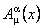 , we obtain the following general field equations: , we obtain the following general field equations:
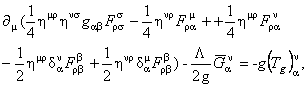 (11) (11)
where 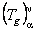 is the gravitational energy-momentum tensor considered as the source of the gravitational field [3, 10]. The expression of this tensor has been obtained using a computing program based on MAPLE system. We will obtain a solution of the field equations (11) considering the case when the gauge potentials have spherical symmetry [1, 4] : is the gravitational energy-momentum tensor considered as the source of the gravitational field [3, 10]. The expression of this tensor has been obtained using a computing program based on MAPLE system. We will obtain a solution of the field equations (11) considering the case when the gauge potentials have spherical symmetry [1, 4] :
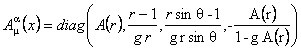 , (12) , (12)
where A (r) is a function of the radial coordinate r only.
1.2. The calculation of the energy-momentum and obtaining of field equations
Using the MAPLE computing program written by us [6, 8] , we obtained the components of tensor 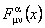 , the metric , the metric 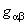 and and 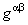 and also of the energy-momentum tensor and also of the energy-momentum tensor 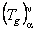 . We list here only a few of the simpler components of the gravitational energy-momentum tensor: . We list here only a few of the simpler components of the gravitational energy-momentum tensor:
 , (13) , (13)
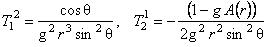 , ,
where 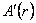 denotes the derivative of the function A (r) with respect to the r variable . Using these expressions, we obtained the following four field equations: denotes the derivative of the function A (r) with respect to the r variable . Using these expressions, we obtained the following four field equations:
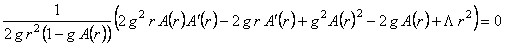 , (14) , (14)
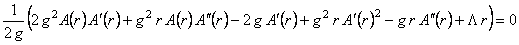 , (15) , (15)
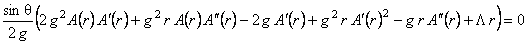 ,(16) ,(16) 
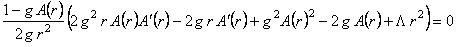 . (17) . (17)
where 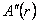 is the derivative of second order of the function is the derivative of second order of the function 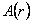 with respect to variable r . with respect to variable r .
1.3. The construction of a solution containing the cosmological constant
It is easy to verify that these equations are equivalent if 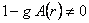 , so that we have only one independent field equation for one unknown function , so that we have only one independent field equation for one unknown function 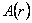 . The constraint . The constraint 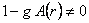 is in accord with the definition (3.1) of the gauge potentials is in accord with the definition (3.1) of the gauge potentials 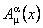 . Denoting . Denoting 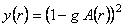 , we obtain from Eq. (14): , we obtain from Eq. (14):
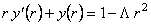 , (18) , (18)
with the solution:
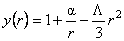 , (4.8) , (4.8)
where a is an arbitrary constant of integration. Then, the solution
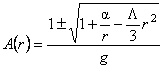 , (20) , (20)
and if we choose 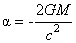 , where M is supposed to be the mass of the point-like source of our gravitational field, then the result (20) corresponds to a Schwarzschild-de-Sitter type solution having the square of the line element [see Eq. (8.a)]: , where M is supposed to be the mass of the point-like source of our gravitational field, then the result (20) corresponds to a Schwarzschild-de-Sitter type solution having the square of the line element [see Eq. (8.a)]:
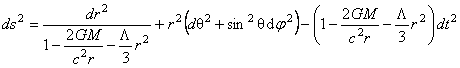 . (21) . (21)
We remember that this line element is defined on the gravitational gauge group space G and that the space-time M remains a Minkowski (flat) one.
The conclusion resulting from the above model is that we can consider the gravitation as a physical interaction in a flat space. The gravitational is described by gauge potentials 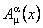 , and the metric is constructed on the manifold of the gravitational gauge group G and do not modify the space-time. As a consequence, It will be easier to obtain quantum models for the gravitational field and, in general for any gauge fields, using the method of integral functional [7], the space-time being flat. , and the metric is constructed on the manifold of the gravitational gauge group G and do not modify the space-time. As a consequence, It will be easier to obtain quantum models for the gravitational field and, in general for any gauge fields, using the method of integral functional [7], the space-time being flat.
Objective 2: Definition of a star product between fields defined on non-commutative space-times
2.1. Construction of gauge-covariant derivative
We consider a non-commutative space-time as base manifold for the gauge theory. This means that the coordinates 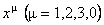 satisfy the following relations of commutation: satisfy the following relations of commutation:
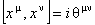 , (22) , (22)
where 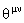 is an anti-symmetric constant matrix. In this case, we have to change the usual product is an anti-symmetric constant matrix. In this case, we have to change the usual product 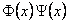 of two field operators by the star product “*” defined as: of two field operators by the star product “*” defined as:
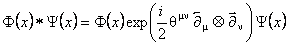 . (23) . (23)
The non-commutative gauge models based on this star product have the disadvantage that they are not Lorentz invariant, i.e. the relation (22) is not invariant under the Lorentz transformations. However, they are invariant under the deformed Poincaré algebra with an abelian twist operator:
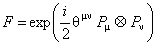 , (24) , (24)
where 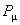 are the generators of the space-time translations which we defined above. The twist P induces a deformed product on the representation space of Poincaré algebra: are the generators of the space-time translations which we defined above. The twist P induces a deformed product on the representation space of Poincaré algebra:
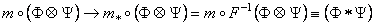 , (25) , (25)
which gives exactly the star product “*” from the definition (23).
Because the “*” product is fixed once for all by the choice of the twist and thus it does not transform at all. As a consequence, there appear difficulties when we try to deform the internal gauge transformations with the same twist (24). It is necessarily to find out a general principle of symmetry so that we can obtain non-commutative internal and external gauge theories without contradictions. Here we describe our results on such a principle [2].
Let us consider the Lie group G as an internal group of symmetry with its Lie algebra 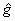 . The infinitesimal generators of the group G are denoted by . The infinitesimal generators of the group G are denoted by 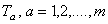 and they satisfy the equations of structure and they satisfy the equations of structure
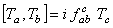 , . (26) , . (26)
where 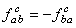 are the structure constants. are the structure constants.
If we suppose that the 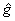 is a local algebra of symmetry (gauge), then a gauge transformation is given by the operator: is a local algebra of symmetry (gauge), then a gauge transformation is given by the operator:
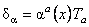 . (27) . (27)
As usually, we introduce the gauge fields, with values into the Lie algebra:
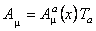 . (28) . (28)
We define the gauge-covariant derivative:
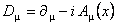 , (29) , (29)
having the property that 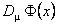 transforms covariant for any field transforms covariant for any field 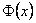 : :
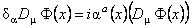 . (30) . (30)
If we want to have a model that includes simultaneously the internal gauge symmetry 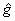 and external P (Poincaré), then we must use the Hopf algebra U ( and external P (Poincaré), then we must use the Hopf algebra U ( 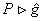 ) associated to the semi-direct product of the two algebras. Then, the gauge covariant derivative have to be written under the form ) associated to the semi-direct product of the two algebras. Then, the gauge covariant derivative have to be written under the form
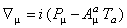 , (31) , (31)
were 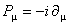 . .
In the work [9] it has been shown that the use of an abelian twist is not compatible with the gauge transformation concept. This is because the ordinary derivative 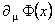 of a field is not gauge-invariant ( i.e. do not transforms like the field themselves). But, using the property (30), we defined in our work [2] a non-abelian twist containing the gauge derivative: of a field is not gauge-invariant ( i.e. do not transforms like the field themselves). But, using the property (30), we defined in our work [2] a non-abelian twist containing the gauge derivative:
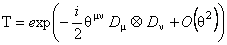 . (32) . (32)
Correspondingly, we defined a new deformed star product 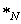 by: by:
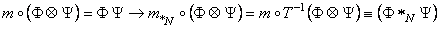 . (33) . (33)
2.2. Verification of the star product properties
In general, this new star product is not associative, so that we have to pay a special attention when we use it. The study of a twist defined with the gauge covariant derivative remains an open question for new researches. However, for some classes of representations of the Hopf algebra U ( 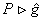 ), the associativity property can be satisfied as we show bellow. ), the associativity property can be satisfied as we show bellow.
Using the Hopf algebra U ( 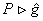 ) as symmetry algebra for the non-commutative gauge theory, we must introduce a co-product ) as symmetry algebra for the non-commutative gauge theory, we must introduce a co-product  , a unity element 1 and a co-unit , a unity element 1 and a co-unit 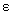 with the properties: with the properties:
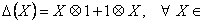  , (34) , (34)
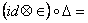 1 = 1 =  . (35) . (35)
The twist operator T must satisfies the conditions:
 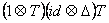 , (36) , (36)
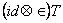 = = 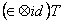 . (37) . (37)
In our works we verified the condition (34) and established that it is satisfied only for those representations of the Hopf algebra U ( 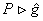 ) which satisfy the constraints: ) which satisfy the constraints:
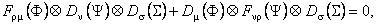 (38) (38)
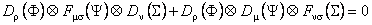 , (39) , (39)
where 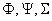 are arbitrary fields from the representation space. are arbitrary fields from the representation space.
The conclusion resulting from our research is that the external Poincaré symmetry and internal gauge symmetry can not be unified under a common twist [2]. This could be a reminiscent of the Coleman-Mandula theorem, although not entirely, since this theorem concerns global symmetry and simple groups. However, the supersymmetry may reverse the situation due to its intrinsic internal symmetry.
2.3. An example of non-commutative model based on Seiberg-Witten map
Using our previous results, we obtained non-commutativity corrections for the metric (21), supposing that 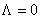 . We used the Seiberg-Witten map [11], and determined the following expressions for the components of the metric up to the second order in the parameter . We used the Seiberg-Witten map [11], and determined the following expressions for the components of the metric up to the second order in the parameter  : :
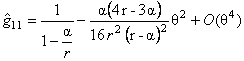 , (40) , (40)
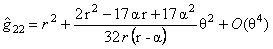 , (41) , (41)
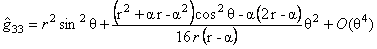 , (42) , (42)
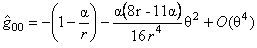 . (43) . (43)
where we chose 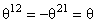 and all other components of and all other components of 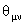 vanishing. We can see that in these expressions we have only corrections of second order in the parameter vanishing. We can see that in these expressions we have only corrections of second order in the parameter 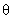 . .
Having these corrections, we can study the thermodynamic properties of a black hole. Some generalizations to other metrics are also possible. These aspects will be studied in the following steps of the project.
References
A. Papers of the research team:
In ISI indexed journals:
- G. Zet , C. Popa , D. Partenie: Schwarzschild-de-Sitter Solution in Quantum Gauge Theory of Gravity, Commun. Theor. Phys. (Beijing, China), Vol. 47 (2007) pp. 843-846 (pdf)
- M. Chaichian, A. Tureanu, G. Zet : Twist as a symmetry principle and noncommutative gauge theory formulation, Phys. Lett. B651 (2007) pp. 319-323 (pdf)
In International Data Basis indexed journals:
- B. Ciobanu , I. Radinschi: Modeling the Energy Distributions of a Dilaton-Maxwell Gravity; va apare în Romanian Journal of Physics Vol. 53 , nr. 1-2 (2008) pp. 29-34 (pdf)
- G. Zet , C. Popa : Spherical gauge gravitation field and spontaneous symmetry breaking, 8-th International Balkan Workshop on Applied Physics, July 5-7, 2007, Constanta; acceptata pentru publicare în Romanian Journal of Physics 2008 (pdf)
- M. Chaichian, M. Setare, A. Tureanu, G. Zet : Noncommutative corrections for spherically symmetric gravitational fields, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- G. Zet , V. Manta , C. Popa : Analytical program for gauge models, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- V. Chiritoiu , G. Zet , S. Babeti: Quantization of gauge fields on de-Sitter group by functional integral method, International Conference on Fundamental and Applied Research in Physics, FARPhys-2007, Iasi 25-27 octombrie 2007; acceptata pentru publicare în Analele Universitatii Al. I. Cuza Iasi, Sectiunea Fizica, 2008 (pdf)
- S. Arustei , V. Manta : Quantum Computation Language Implementation of the Berstein-Vazirani Algorithm, 9-th International Symposium on Automatic Control and Computer Science, Iasi, November 16-17, 2007, Proceedings Ed. Politehnium, 2007, p. 179-182, ISSN 1843-7257; acceptata pentru publicare în Buletinul Institutului Politehnic Iasi, fasc. 1-4 Automatica si calculatoare, 2007 (pdf)
B. Papers of other authors:
- M. Chaichian, A Tureanu: Twist Symmetry and Gauge Invariance, Phys. Lett. B637 (2006) pp. 199-202
- N. Wu: Renormalizable Quantum Gauge Theory of Gravity, Commun. Theor. Phys. (Beijing, China), Vol. 38 (2002) pp. 151-156
- N. Seiberg, E. Witten: String Theory and Noncommutativity Geometry, JHEP 9909 (1999) 032
PDF format of stage 1 synthesis
|