Stage 2
01.01.2008 - 31.12.2008
Objective 1. Formulation of the general gauge theory with 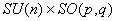 as structural group as structural group
1.1. Obtaining the structure equations of the gauge group
The SO(p, q) group has the dimension equal to m ( m -1)/2 where m = p + q , and the SU(n) group is non-abelian, having the dimension 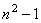 . The infinitesimal generators of the SO(p, q) group are denoted by . The infinitesimal generators of the SO(p, q) group are denoted by 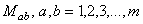 and those of SU(n) group by and those of SU(n) group by 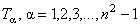 . Generally, . Generally, 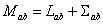 , where , where 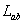 are the angular momentum operators and are the angular momentum operators and 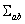 denotes the spin operators in the considered representation. The equations of structure have the form [2, 7]: denotes the spin operators in the considered representation. The equations of structure have the form [2, 7]:
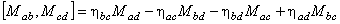 , (1.1a) , (1.1a)
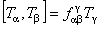 , (1.1b) , (1.1b)
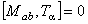 , (1.1c) , (1.1c)
where
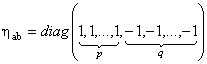
is the m -dimensional Lorentz metric, and 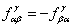 are the structure constants of the group are the structure constants of the group 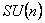 . In the particular case of the group . In the particular case of the group 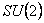 the structure constants coincides with the total anti-symmetric tensor the structure constants coincides with the total anti-symmetric tensor 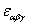 having the property having the property 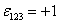 . The equation (1.1c) shows that the group . The equation (1.1c) shows that the group 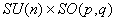 has a direct product structure. In order to describe the gravitational field we will choose has a direct product structure. In order to describe the gravitational field we will choose 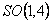 as gauge group whose dimension is as gauge group whose dimension is 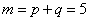 . Therefore, we have . Therefore, we have 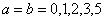 , or denoting , or denoting 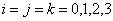 we can write we can write 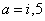 etc. etc.
1.2. Definition of the gauge invariant derivative
We define now the gauge covariant derivative, associated to the local group of symmetry SU(n) 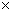 SO(p, q) [2]: SO(p, q) [2]:
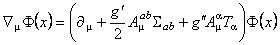 , (1.2) , (1.2)
where 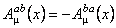 are the are the 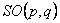 gauge potentials describing the gravitational field, and gauge potentials describing the gravitational field, and 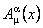 are the internal gauge potentials associated to the group SU(n). The quantities are the internal gauge potentials associated to the group SU(n). The quantities 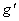 and and 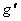 denote the coupling constants of the gravitational and respectively internal SU(n) gauge fields. In the particular case of the group denote the coupling constants of the gravitational and respectively internal SU(n) gauge fields. In the particular case of the group 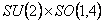 the potentials the potentials 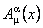 correspond to the isospin states and correspond to the isospin states and 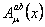 decompose in two parts: the spin connection decompose in two parts: the spin connection 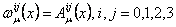 and the tetrads and the tetrads 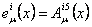 . .
1.3. Obtaining the general expressions of the tensors associated to gauge potentials
In order to determine the tensors associated to gauge potentials 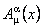 and and 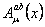 , we calculate the commutator , we calculate the commutator 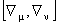 . Using the equations of structure (1.1), we obtain [7]: . Using the equations of structure (1.1), we obtain [7]:
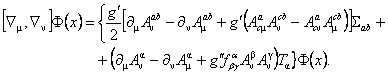 (1.3) (1.3)
If we use the general definition
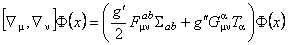 , (1.4) , (1.4)
and identify the Eqs. (1.3) and (1.4), then we obtain
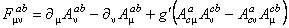 , (1.5) , (1.5)
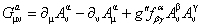 . (1.6) . (1.6)
In particular, if we consider the case of SU(2) 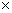 SO(1, 4), chose SO(1, 4), chose 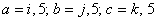 with with 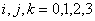 and denote and denote 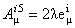 , then the Eq. (1.5) becomes [10] , then the Eq. (1.5) becomes [10]
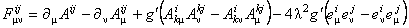 , (1.7) , (1.7)
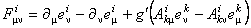 . (1.8) . (1.8)
In a Riemann-Cartan model the quantities 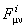 are interpreted as the components of the torsion tensor are interpreted as the components of the torsion tensor 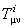 , and , and 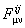 as the components of the curvature tensor as the components of the curvature tensor 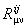 of the space-time. of the space-time.
Objective 2: Obtaining the field equations for the gauge potentials
2.1. Construction of the action integral for the gauge potentials
The potentials 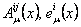 describe the gravitational field and describe the gravitational field and 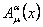 - the internal properties (isospin, hypercharge, etc) of the considered physical system. The tetrads - the internal properties (isospin, hypercharge, etc) of the considered physical system. The tetrads 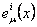 can be used to define a metric tensor can be used to define a metric tensor
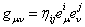 , (2.1) , (2.1)
where 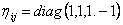 is the Lorentz metric. The gauge potentials allow to define the integral of the action of the considered model. It contains two terms, one corresponding to the sector SO(p, q) and the other to the is the Lorentz metric. The gauge potentials allow to define the integral of the action of the considered model. It contains two terms, one corresponding to the sector SO(p, q) and the other to the 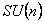 sector: sector:
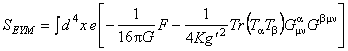 . (2.2) . (2.2)
In this expression we used the definitions
 , (2.3) , (2.3)
where 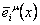 denotes the inverse of denotes the inverse of 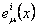 , i.e. , i.e.
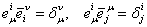 . (2.4) . (2.4)
From now on we choose 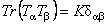 and and 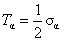 , where , where 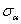 denotes the Pauli matrices. denotes the Pauli matrices. 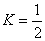 . The gravitational constant G in (2.2) is the only dimensional quantity in action, because we will use the units . The gravitational constant G in (2.2) is the only dimensional quantity in action, because we will use the units 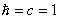 . .
2.2. Obtaining the field equations by the variational method
We impose the condition 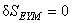 (the variational principle) with respect to (the variational principle) with respect to 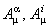 and and 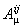 . Then we obtain respectively the following field equations: . Then we obtain respectively the following field equations:
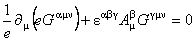 , (2.5) , (2.5)
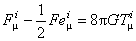 , (2.6) , (2.6)
where 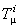 is the energy-momentum tensor [3, 7] of the gauge fields is the energy-momentum tensor [3, 7] of the gauge fields 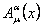
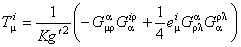 , (2.7) , (2.7)
and respectively
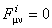 . (2.8) . (2.8)
In the case of the group 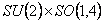 the equations (2.5) determine the isospin states, those from (2.6) correspond to the Einstein equations, and (2.8) shows that we have a space without torsion. They are known as Einstein-Yang-Mills equations (EYM). By integrating the equations EYM we obtain the gauge potentials as solutions. the equations (2.5) determine the isospin states, those from (2.6) correspond to the Einstein equations, and (2.8) shows that we have a space without torsion. They are known as Einstein-Yang-Mills equations (EYM). By integrating the equations EYM we obtain the gauge potentials as solutions.
2.3 Formulation of the self-duality conditions
We can obtain easier solutions of the field equations if we impose the self-duality condition for the tensor of the gauge fields. To do that we define the dual tensors
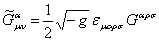 , (2.9) , (2.9)
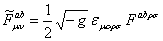 . (2.10) . (2.10)
where  , , 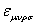 is the total anti-symmetric Levi-Civita tensor ( is the total anti-symmetric Levi-Civita tensor ( 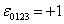 ) and ) and
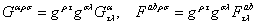 . (2.11) . (2.11)
Then, the self-duality condition is given by the relations
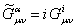 , , 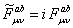 . (2.12) . (2.12)
These are equations of the first order in contrast with the equations EYM which are of second order and the obtaining of their solutions is easier. Any solution of the self-duality equations (2.12) is also a solution of the EYM equations but reverse is not true.
Objective 3: Applications to the spherically symmetric case
3.1. Obtaining spherically symmetric solutions
For the spherically symmetric case, the Minkowski space-time is endowed with the metric
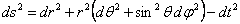 . (3.1) . (3.1)
We present now three examples of solutions of the previous field equations.
1) Solution with cosmological constant
We consider, as an example, the particular form of spherically gauge fields of the SO(1,4) group given by the following ansatz:
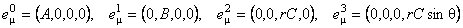 , (3.2) , (3.2)
and
 (3.3) (3.3)
where A, B, C, U, V, Z and W are functions only of the three-dimensional radius r . In addition, the spherically symmetric SU(2) gauge fields will be parametrized as:
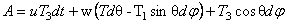 , (3.4) , (3.4)
where u and 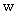 are functions also depending only of variable r . Then, imposing the constraints are functions also depending only of variable r . Then, imposing the constraints 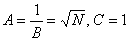 where N ( r ) is a new unknown positive defined function, we obtain: where N ( r ) is a new unknown positive defined function, we obtain:
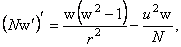
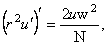 (3.5) (3.5)
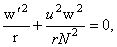
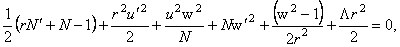
where we used 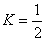 and and 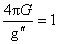 units. These equations admit the following solution (Schwarzschild-Reissner-Nordstrom-de-Sitter) with a nontrivial gauge field describing colored black holes [4, 5, 6]: units. These equations admit the following solution (Schwarzschild-Reissner-Nordstrom-de-Sitter) with a nontrivial gauge field describing colored black holes [4, 5, 6]:
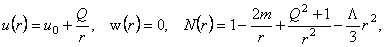 (3.6) (3.6)
where 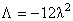 is the cosmological constant of the model. The equations (3.5) admit also the self-dual solution (Schwarzschild): is the cosmological constant of the model. The equations (3.5) admit also the self-dual solution (Schwarzschild):
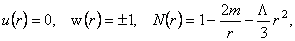 (3.7) (3.7)
But, the solution (3.6) is not a self-dual one.
Making a contraction 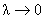 of the SO(1, 4) group, we obtain the Poincaré gauge theory coupled with the isospin group SU(2). The solutions of the field equations are given by (3.6) and (3.7) where of the SO(1, 4) group, we obtain the Poincaré gauge theory coupled with the isospin group SU(2). The solutions of the field equations are given by (3.6) and (3.7) where 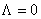 . Therefore, the Poincaré gauge theory do not allows a cosmological constant. . Therefore, the Poincaré gauge theory do not allows a cosmological constant.
2) Model with the quantum gauge group 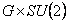
The gauge gravitational group 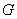 has the generators has the generators 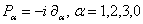 considered as differential operators which commutes [12]: considered as differential operators which commutes [12]:
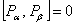 . (3.8) . (3.8)
The generators of 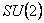 are denoted by are denoted by 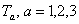 and they satisfy of the form given in (1.1b). The internal and gravitational gauge fields with values in the Lie algebra are: and they satisfy of the form given in (1.1b). The internal and gravitational gauge fields with values in the Lie algebra are:
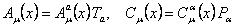 . (3.9) . (3.9)
We choose the spherically symmetric gauge fields in the form [1]:
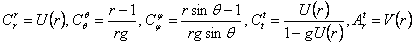 , (3.10) , (3.10)
where 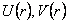 are functions depending only of r and g is the gravitational coupling constant. Then, the corresponding field equations are [1] are functions depending only of r and g is the gravitational coupling constant. Then, the corresponding field equations are [1]
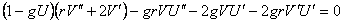 , (3.11) , (3.11)
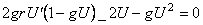 . (3.12) . (3.12)
The general solution of the equation (3.12) is [1]
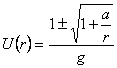 , (3.13) , (3.13)
where a is an arbitrary constant of integration. Choosing a = - 2 Gm , the solution (3.13)gives the Schwarzschild metric [1]:
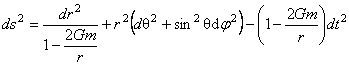 . (3.14) . (3.14)
Then, we obtain from (3.11) two corresponding solutions for 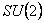 gauge potentials: gauge potentials:
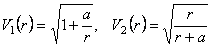 . (3.15) . (3.15)
These results show that there are only gravitational couplings into the considered model but no 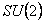 internal couplings because the solution we obtained do not contains the internal couplings because the solution we obtained do not contains the 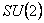 coupling constant. coupling constant.
The model presented here allows the quantization of the gravitational field by using path integral method [10] on the same way as for internal gauge theories. Because the gauge group G is considered here as a pure internal symmetry, the property of renormalization is assured for our unified gauge model [1, 10].
3) Solutions for gauge fields on non-commutative space-time
We suppose now that the space-time is non-commutative with the coordinates 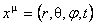 satisfying the following commutation relations: satisfying the following commutation relations:
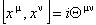 , (3.16) , (3.16)
where 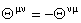 are constant parameters. We will consider the space-space non-commutativity [2] when the only non-vanishing components are are constant parameters. We will consider the space-space non-commutativity [2] when the only non-vanishing components are 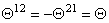 , where , where 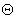 is a constant parameter of deformation. To describe different gauge fields we use the star product is a constant parameter of deformation. To describe different gauge fields we use the star product 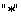 defined by relation [2, 3]: defined by relation [2, 3]:
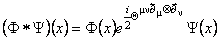 . (3.17) . (3.17)
Let us suppose now that the gauge group is 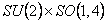 and denote the gauge fields (potentials) by and denote the gauge fields (potentials) by 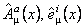 . We define the metric of the non-commutative space-time as . We define the metric of the non-commutative space-time as
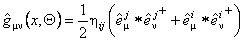 , (3.18) , (3.18)
Then,using the Witten-Seiberg map [2, 3, 13], we obtain the following corrections [2, 3]:
• for the internal 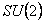 gauge fields (with the commutative solution (3.7)): gauge fields (with the commutative solution (3.7)):
 (3.19) (3.19)
• for the Schwarzschild metric
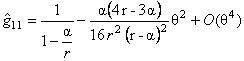 , ,
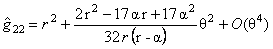 , (3.20) , (3.20)
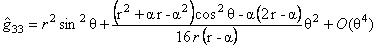 , ,
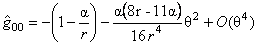 , ,
where 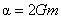 . These solutions can be used to the determination of some quantum characteristics of the black holes such as temperature, entropy, etc. . These solutions can be used to the determination of some quantum characteristics of the black holes such as temperature, entropy, etc.
3.2. Establishing conditions non-singular solutions of the field equations
We construct now an integral of the action of the gauge fields 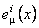 under the form [2, 14]: under the form [2, 14]:
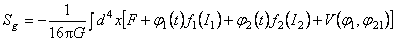 , (3.21) , (3.21)
where 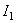 and and 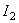 are two invariants of theory, and are two invariants of theory, and  , , 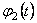 are Lagrange multipliers introduced in order to assure the existence of nonsingular solutions. The potentials are Lagrange multipliers introduced in order to assure the existence of nonsingular solutions. The potentials 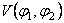 satisfy the conditions: satisfy the conditions:
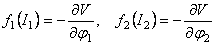 . (3.22) . (3.22)
A possible form of the functions 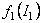 and and 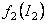 is [14]: is [14]:
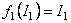 , , 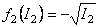 , , 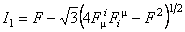 , , 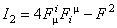 . (3.23) . (3.23)
If we know the metric of the space-time, we can determine then the functions 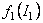 , , 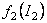 and the potential and the potential 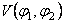 . .
3.3. Construction of a non-singular solution
We consider the case of the Robertson-Walker metric
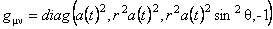
and suppose that 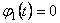 . We denote . We denote 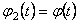 and respectively and respectively 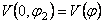 . Then, imposing the variational principle . Then, imposing the variational principle 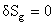 with respect to with respect to 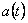 and and 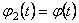 , we obtain the following conditions which assure the existence of non-singular solutions: , we obtain the following conditions which assure the existence of non-singular solutions:
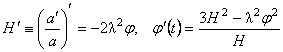 . (3.24) . (3.24)
where 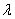 is the deformation parameter of the Lie algebra [see eq. (1.8)]. These equations admit the periodic solution: is the deformation parameter of the Lie algebra [see eq. (1.8)]. These equations admit the periodic solution:
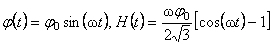 , (3.25) , (3.25)
where 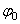 is an integration constant and is an integration constant and 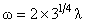 is the frequency of the gravitational field described by the gauge fields is the frequency of the gravitational field described by the gauge fields 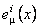 and and 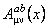 . This solution has no singularities and is associated with a negative cosmological constant . This solution has no singularities and is associated with a negative cosmological constant 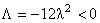 . The case when this constant is positive can be studied analogous by using the anti-de-Sitter group . The case when this constant is positive can be studied analogous by using the anti-de-Sitter group 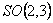 . .
It is possible to obtain and other solutions without singularities supposing that the cosmological “constant” itself has a dependence of time. Using the method described in this section we can obtain non-singular solutions for case of gauge theories with internal groups of symmetry.
References
A. Papers of the research team:
- in ISI indexed journals
- G. Zet, V. Manta, C. Popa: Gauge Model Based on Group
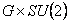 , Chin. Phys. Lett. Vol. 25 No.2 (2008) p. 433-435 (pdf) , Chin. Phys. Lett. Vol. 25 No.2 (2008) p. 433-435 (pdf)
- M. Chaichian, A. Tureanu, G. Zet: Corrections to Schwarzschild solution in non-commutative gauge theory of gravitation, Phys. Lett. B660 (2008) p. 573-578 (pdf)
- in International Data Basis indexed journals
- G. Zet: Unified Gauge Theory on Non-commutative space-time, Rom. J. Phys. Vol. 53 , No. 5-6 (2008) p. 635-644 (pdf)
- G. Zet, C. Popa: Spherical Gauge Gravitational Field and Spontaneous Symmetry Breaking , Rom. J. Phys. Vol. 53 , No. 5-6 (2008) p. 621-634 (pdf)
- G. Zet, C. Popa, D. Partenie: Gauge Symmetry of Gravitation, Bul. Inst. Politehnic Ia s i, Tom LIII ( LVII ), fasc. 1-2, Sectia Matematica. Mecanica Teoretica. Fizica (2007) p.103-114 (pdf)
- B. Ciobanu, I. Radinschi: Modeling the Electric and Magnetic Fields in Rotating Universe, Rom. J. Phys. Vol. 53 , No. 1-2 (2008) p. 405-416 (pdf)
- G. Zet, V. Manta : Gauge Theory with
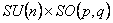 as structure group, Bul. Inst. Politehnic Iasi, acceptata pentru publicare 2008 (pdf) as structure group, Bul. Inst. Politehnic Iasi, acceptata pentru publicare 2008 (pdf)
- presented at national and international conferences
- G. Zet: General relativistic analog solutions for Yang-Mills theory on noncommutative space-time, Conferinta Nationala de Fizica Teoretica (CNFT3) 10-13 Iunie 2008, Busteni, Romania (pdf)
- G. Zet: U(2) gauge theory on non-commutativity geometry, Second Workshop on Quantum Gravity, 22-24 Septembrie 2008, Lusofona University, Lisbon
- V. Chiritoiu, G. Zet: Renormalization in Quantum Gauge Theory, Conferinta Nationala de Fizica, 10-13 Septembrie 2008, Bucuresti-Magurele
B. Other authors' papers
-
M Blagojevic: Gravitation and Gauge Symmetry. IOP Publishing 2008
-
N. Wu: Renormalizable Quantum Gauge Theory of Gravity, Commun. Theor. Phys. 38 (2002) p. 151-156
-
N.Seiberg, E. Witten : String Theory and Noncommutativity Geometry JHEP 9909 (2008) 032
C. Previously published papers of the research team
-
G. Zet, C.D. Oprisan, S. Babeti: Solutions without singularities in gauge theory of gravitation, Int. J. Mod. Phys. 15C (2004) p. 1031-1038
PDF format of stage 2 synthesis |