Etapa 2: 01.01.2008 - 31.12.2008
Raport anual de activitate - 2008
S I N T E Z A
Obiectivul 1: Formularea teoriei gauge generale cu grupul structural 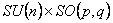
1.1. Obtinerea ecuatiilor de structura ale grupului gauge
Grupul 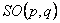 are dimensiunea egala cu m ( m -1)/2 unde m = p + q , iar grupul are dimensiunea egala cu m ( m -1)/2 unde m = p + q , iar grupul 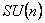 este ne-abelian, având dimensiunea este ne-abelian, având dimensiunea 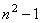 . Generatorii infinitezimali ai grupului . Generatorii infinitezimali ai grupului 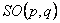 sunt notati prin sunt notati prin 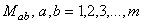 , iar cei ai lui , iar cei ai lui 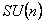 prin prin 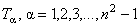 . În general, . În general, 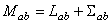 , unde , unde 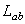 sunt operatorii momentului cinetic, iar sunt operatorii momentului cinetic, iar 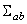 noteaza generatorii de spin în reprezentarea considerata. Ecuatiile de structura ale grupului noteaza generatorii de spin în reprezentarea considerata. Ecuatiile de structura ale grupului 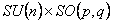 sunt [2, 7]: sunt [2, 7]:
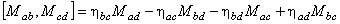 , (1.1a) , (1.1a)
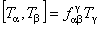 , (1.1b) , (1.1b)
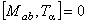 , (1.1c) , (1.1c)
unde
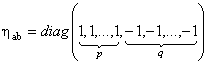
este metrica Lorentz m -dimensionala, iar 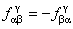 sunt constantele de structura ale grupului sunt constantele de structura ale grupului 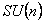 . În cazul particular al grupului . În cazul particular al grupului 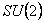 constantele de structura constantele de structura 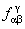 coincid cu tensorul complet anti-simetric coincid cu tensorul complet anti-simetric 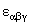 , cu proprietatea , cu proprietatea 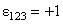 . Ecuatia (1.1c) arata ca grupul . Ecuatia (1.1c) arata ca grupul 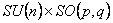 are structura unui produs direct. Pentru a descrie câmpul gravitational vom alege grupul gauge are structura unui produs direct. Pentru a descrie câmpul gravitational vom alege grupul gauge 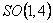 , care are dimensiunea , care are dimensiunea 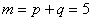 . Deci, vom avea . Deci, vom avea 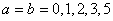 , sau notând , sau notând 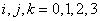 , vom scrie , vom scrie 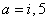 etc. etc.
1.2. Definirea derivatei gauge invarianta
Definim derivatei gauge invarianta asociata grupului de simetrie locala 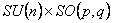 prin relatia [2] prin relatia [2]
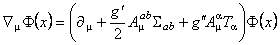 , (1.2) , (1.2)
unde 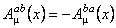 sunt potentialele gauge sunt potentialele gauge 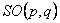 care descriu câmpul gravitational, iar care descriu câmpul gravitational, iar 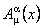 sunt potentialele gauge interne asociate grupului sunt potentialele gauge interne asociate grupului 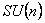 . Cantitatile . Cantitatile 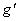 si si 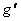 noteaza constantele de cuplaj ale interactiunilor gravitationala si respectiv a câmpurilor gauge interne. noteaza constantele de cuplaj ale interactiunilor gravitationala si respectiv a câmpurilor gauge interne.
În cazul particular al grupului 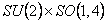 , potentialele , potentialele 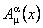 corespund starilor de izospin, iar corespund starilor de izospin, iar 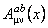 se descompun în doua parti: conexiunea de spin se descompun în doua parti: conexiunea de spin 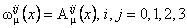 si tetrazii si tetrazii 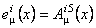 . .
1.3. Obtinerea expresiilor generale ale tensorilor asociati potentialelor gauge
Pentru a determina tensorii asociati câmpurilor gauge 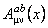 si si 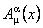 , vom calcula comutatorul , vom calcula comutatorul 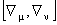 . Folosind ecuatiile de structura (1.1) obtinem [7]: . Folosind ecuatiile de structura (1.1) obtinem [7]:
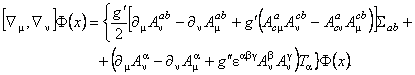 (1.3) (1.3)
Daca folosim definitia generala
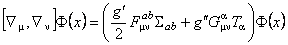 , (1.4) , (1.4)
si identificam ecuatiile (1.3) si (1.4), atunci rezulta
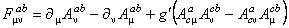 , (1.7) , (1.7)
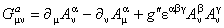 . (1.6) . (1.6)
În cazul particular SU(2) 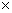 SO(1,4), alegem SO(1,4), alegem 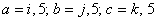 , cu , cu 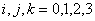 si notam si notam 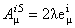 ; atunci ecuatia (2.6) devine[10]: ; atunci ecuatia (2.6) devine[10]:
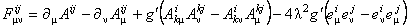 , (1.7) , (1.7)
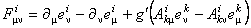 . (1.8) . (1.8)
Pentru un model Riemann-Cartan, cantitatile 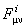 sunt interpretate drept componentele torsiunii sunt interpretate drept componentele torsiunii 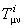 , iar , iar 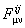 - ale curburii - ale curburii 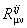 spatiului-timp. spatiului-timp.
Obiectivul 2: Obtinerea ecuatiilor de câmp pentru potentialele gauge
2.1. Construirea integralei actiunii pentru potentialele gauge
Potentialele gauge 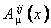 , , 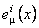 descriu câmpul gravitational, iar descriu câmpul gravitational, iar 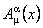 - proprietatile interne (izoapinul, hipersarcina, etc.) ale sistemului fizic considerat. Tetrazii - proprietatile interne (izoapinul, hipersarcina, etc.) ale sistemului fizic considerat. Tetrazii 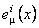 pot fi folositi pentru a defini un tensor metric: pot fi folositi pentru a defini un tensor metric:
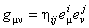 , (2.1) , (2.1)
unde 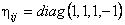 este metrica Lorentz. este metrica Lorentz.
Cu ajutorul potentialelor gauge construim integrala actiunii pentru modelul considerat. Aceasta contine doi termeni, unul corespunzator sectorului 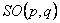 si celalalt sectorului si celalalt sectorului 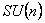 : :
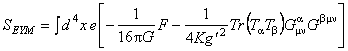 . (2.2) . (2.2)
În aceasta expresie am folosit definitiile:
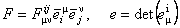 , (2.3) , (2.3)
unde 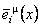 noteaza inversul lui noteaza inversul lui 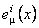 , adica , adica
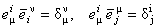 . (2.4) . (2.4)
În cele ce urmeaza vom alege 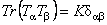 si si 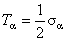 , unde , unde 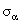 sunt matricele lui Pauli. Constanta gravitationala G din (2.2) este singura cantitate dimensionala, deoarece vom alege sistemul de unitati sunt matricele lui Pauli. Constanta gravitationala G din (2.2) este singura cantitate dimensionala, deoarece vom alege sistemul de unitati 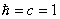 . .
2.2. Obtinerea ecuatiilor de câmp prin metoda variationala
Impunem conditia 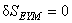 (principiul variational) în raport cu potentialele (principiul variational) în raport cu potentialele 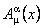 , , 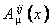 , , 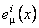 . Atunci, obtinem urmatoarele ecuatii de câmp . Atunci, obtinem urmatoarele ecuatii de câmp
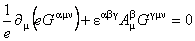 , (2.5) , (2.5)
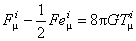 , (2.6) , (2.6)
unde 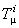 este tensorul energie-impuls [3, 7] al câmpurilor gauge este tensorul energie-impuls [3, 7] al câmpurilor gauge 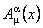
 , (2.7) , (2.7)
si respectiv
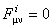 . (2.8) . (2.8)
În cazul grupului 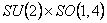 , ecuatiile (2.5) determina starile de izospin, cele din (2.6) corespund ecuatiilor lui Einstein, iar (2.8) arata ca avem un spatiu fara torsiune. Ele sunt cunoscute sub denumirea de ecuatiile Einstein-Yang-Mills (EYM). Prin integrarea ecuatiilor EYM se obtin potentialele gauge ca solutii. , ecuatiile (2.5) determina starile de izospin, cele din (2.6) corespund ecuatiilor lui Einstein, iar (2.8) arata ca avem un spatiu fara torsiune. Ele sunt cunoscute sub denumirea de ecuatiile Einstein-Yang-Mills (EYM). Prin integrarea ecuatiilor EYM se obtin potentialele gauge ca solutii.
2.3. Formularea conditiei de auto-dualitate
Se pot obtine mai usor solutii ale ecuatiilor de câmp daca impunem conditia de auto-dualitate pentru tensorul câmpurilor gauge. Pentru aceasta definim tensorii duali
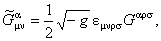 (2.9) (2.9)
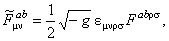 (2.10) (2.10)
unde 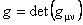 , , 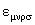 este tensorul Levi-Civita complet anti-simetric ( este tensorul Levi-Civita complet anti-simetric ( 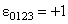 ) si ) si
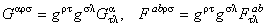 . (2.11) . (2.11)
Atunci, conditia de auto-dualitate înseamna satisfacerea relatiilor:
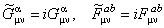 . (2.12) . (2.12)
Acestea sunt ecuatii diferentiale de ordinul întâi, spre deosebire de ecuatiile EYM care sunt de ordinul al doilea si obtinerea solutiilor pentru ele este mai simpla. Orice solutie a ecuatiilor de auto-dualitate (2.12) este si solutie a ecuatiilor EYM dar nu si invers.
Obiectivul 3: Aplicatii la cazul simetriei sferice
3.1. Obtinerea unor solutii cu simetrie sferica
În cazul simetriei sferice spatiul-timp Minkowski este dotat cu metrica
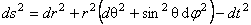 . (3.1) . (3.1)
Vom prezenta trei exemple de solutii obtinute pe baza rezultatelor anterioare.
1) Solutii cu constanta cosmologica.
Consideram cazul când câmpurile gauge 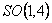 au forma [2, 3, 7] : au forma [2, 3, 7] :
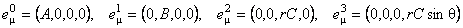 , (3.2) , (3.2)
si
 (3.3) (3.3)
unde A, B, C, U, V, Z si W sunt functii numai de variabila r . În plus, vom parametriza câmpurile gauge 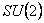 astfel: astfel:
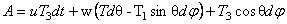 , (3.4) , (3.4)
unde u si w sunt, de asemenea, functii numai de r . Atunci. Considerând constrângerile 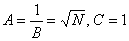 , unde N ( r ) este o noua functie pozitiv definita, obtinem: , unde N ( r ) este o noua functie pozitiv definita, obtinem:
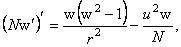 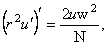 (3.5) (3.5)
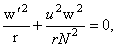
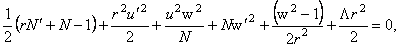
unde am folosit 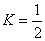 si unitati si unitati 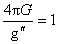 . Aceste ecuatii admit urmatoarea solutie (Schwarzschild-Reissner-Nordström-de-Sitter ) de tipul black hole color [4,5,6]: . Aceste ecuatii admit urmatoarea solutie (Schwarzschild-Reissner-Nordström-de-Sitter ) de tipul black hole color [4,5,6]:
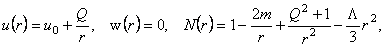 (3.6) (3.6)
unde 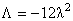 este constanta cosmologica. Ecuatiile (3.5) admit si solutia (Schwarzschild-deSitter) auto-duala: este constanta cosmologica. Ecuatiile (3.5) admit si solutia (Schwarzschild-deSitter) auto-duala:
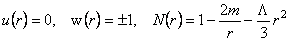 . (3.7) . (3.7)
Spre deosebire de acesta, solutia (3.6) nu este auto-duala.
Prin contractia 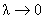 , grupul , grupul 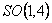 trece în grupul Poincaré cuplat cu grupul izospinului. Solutiile ecuatiilor de câmp sunt date în acest caz de (3.6) si (3.7) în care trebuie sa luam trece în grupul Poincaré cuplat cu grupul izospinului. Solutiile ecuatiilor de câmp sunt date în acest caz de (3.6) si (3.7) în care trebuie sa luam 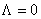 . Deci, teoria gauge Poincaré nu admite o constanta cosmologica. . Deci, teoria gauge Poincaré nu admite o constanta cosmologica.
2) Model bazat pe grupul gauge cuantic 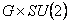
Grupul gauge gravitational G are generatorii 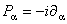 , , 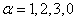 , considerati ca operatori diferentiali si care comuta între ei [12]: , considerati ca operatori diferentiali si care comuta între ei [12]:
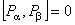 . (3.8) . (3.8)
Generatorii grupului SU (2) sunt notati prin 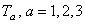 si satisfac relatii de comutare ca în (1.1b). Câmpurile gauge interne si gravitationale cu valori în algebra Lie sunt: si satisfac relatii de comutare ca în (1.1b). Câmpurile gauge interne si gravitationale cu valori în algebra Lie sunt:
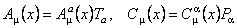 . (3.9) . (3.9)
Alegem aceste câmpuri gauge cu simetrie sferica, de forma [1]
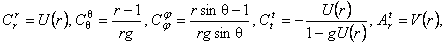 (3.10) (3.10)
unde U, V sunt functii numai de r , iar g este constanta de cuplaj gravitationala. Atunci, ecuatiile de câmp corespunzatoare sunt [1] :
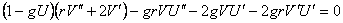 , (3.11) , (3.11)
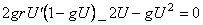 . (3.12) . (3.12)
Solutia generala a ecuatiei (3.12) este [1] :
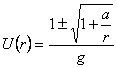 , (3.13) , (3.13)
unde a este o constanta arbitrara de integrare. Alegând a = - 2 Gm , solutia (3.13) conduce la metrica Schwarzschild [1] :
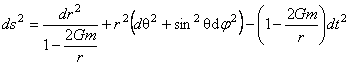 . (3.14) . (3.14)
Corespunzator, din (3.11) obtinem doua solutii pentru potentialele gauge SU (2):
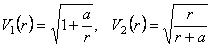 . (3.15) . (3.15)
Aceste rezultate arata ca, în cazul considerat, exista numai cuplaj gravitational între câmpuri, dar nu si cuplaje interne SU (2), deoarece solutiile obtinute nu contin constanta de cuplaj a lui SU (2).
Modelul prezentat permite cuantificarea câmpului gravitational prin metoda integralei functionale [10] ca în cazul teoriilor gauge interne. Deoarece grupul gauge G se considera aici ca o simetrie pur interna, proprietatea de re-normare este asigurata pentru modelul nostru gauge de unificare [1,10].
3 ) Solutie pentru câmpurile gauge pe spatii-timp necomutative.
Presupunem ca spatiul-timp este ne-comutativ, având coordonatele 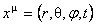 care satisfac urmatoarele relatii de comutare: care satisfac urmatoarele relatii de comutare:
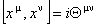 , (3.16) , (3.16)
unde 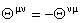 sunt parametrii constanti ai modelului. Vom alege cazul ne-comutativitatii spatiu-spatiu [2], si vom presupune ca singurele componente ne-nule sunt sunt parametrii constanti ai modelului. Vom alege cazul ne-comutativitatii spatiu-spatiu [2], si vom presupune ca singurele componente ne-nule sunt 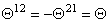 , unde , unde 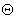 este un parametru constant de deformare. Pentru descrierea diferitelor câmpuri gauge folosim produsul star este un parametru constant de deformare. Pentru descrierea diferitelor câmpuri gauge folosim produsul star 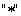 , definit prin relatia [2, 3] : , definit prin relatia [2, 3] :
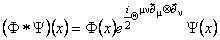 . (3.17) . (3.17)
Presupunem apoi ca grupul gauge este 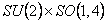 si notam câmpurile (potentialele) gauge pe spatiul-timp ne-comutativ prin si notam câmpurile (potentialele) gauge pe spatiul-timp ne-comutativ prin 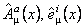 . Definim metrica spatiului-timp ne-comutativ prin relatia: . Definim metrica spatiului-timp ne-comutativ prin relatia:
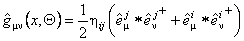 . (3.18) . (3.18)
Folosind aplicatia Seiberg-Witten [2, 3, 13], obtinem urmatoarele corectii [2, 3]:
- pentru câmpurile gauge SU (2) interne (cu solutia comutativa (3.7)):
 (3.19) (3.19)
- pentru metrica Schwarzschild:
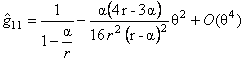 , ,
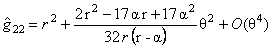 , (3.20) , (3.20)
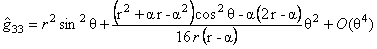 , ,
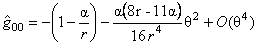 , ,
unde 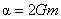 . Aceste solutii sunt utile pentru determinarea unor caracteristici cuantice ale gaurilor negre ( black holes ) cum ar fi temperatura, entropia, etc. . Aceste solutii sunt utile pentru determinarea unor caracteristici cuantice ale gaurilor negre ( black holes ) cum ar fi temperatura, entropia, etc.
3.2. Stabilirea conditiilor ca ecuatiile de câmp sa admita solutii ne-singulare
Construim integrala actiunii câmpurilor gauge 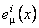 sub forma [2, 14] : sub forma [2, 14] :
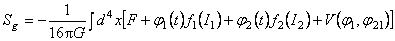 , (3.21) , (3.21)
unde 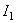 si si 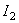 sunt doi invarianti ai teoriei, iar sunt doi invarianti ai teoriei, iar 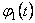 si si 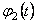 sunt multiplicatori Lagrange introdusi pentru a asigura existenta unor solutii fara singularitati. Potentialul sunt multiplicatori Lagrange introdusi pentru a asigura existenta unor solutii fara singularitati. Potentialul 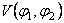 satisface conditiile: satisface conditiile:
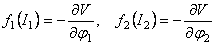 . (3.22) . (3.22)
O alegere corespunzatoare a functiilor 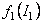 si si 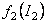 este [14]: este [14]:
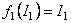 , , 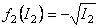 , , 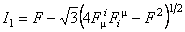 , , 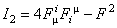 . (3.23) . (3.23)
Cunoscând metrica spatiului-timp, cu relatiile (3.22) si (3.23) determinam functiile 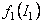 , , 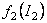 si potentialul si potentialul 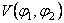 . .
3.3 Construirea solutiilor gauge nesingulare .
Vom considera cazul metricii Robertson-Walker 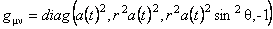 si vom presupune si vom presupune 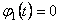 . Notam . Notam 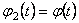 si corespunzator si corespunzator 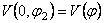 . Atunci, impunând principiul variational . Atunci, impunând principiul variational 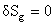 în raport cu în raport cu 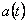 si si 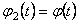 , obtinem urmatoarele conditii care asigura existenta solutiilor ne-singulare: , obtinem urmatoarele conditii care asigura existenta solutiilor ne-singulare: 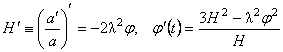 , (3.24) , (3.24)
unde 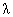 este parametrul de deformare [3, 4] al algebrei Lie [vezi (1.8)]. Aceste ecuatii admit solutia periodica: este parametrul de deformare [3, 4] al algebrei Lie [vezi (1.8)]. Aceste ecuatii admit solutia periodica:
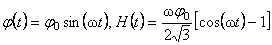 , (3.25) , (3.25)
unde 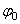 este o constanta de integrare si este o constanta de integrare si 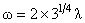 este frecventa de oscilatie a câmpului gravitational descris de câmpurile gauge este frecventa de oscilatie a câmpului gravitational descris de câmpurile gauge 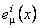 si si 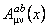 . Aceasta solutie nu are singularitati si este valabila pentru cazul unei constante cosmologice negative: . Aceasta solutie nu are singularitati si este valabila pentru cazul unei constante cosmologice negative: 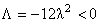 . Pentru a trata cazul unei constante cosmologice pozitive, trebuie sa folosim grupul anti-de-Sitter . Pentru a trata cazul unei constante cosmologice pozitive, trebuie sa folosim grupul anti-de-Sitter 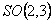 . .
Este posibil sa se obtina si alte solutii ne-singulare, presupunând o dependenta de timp a „constantei” cosmologie. În mod analog se pot determina solutii ne-singulare în cazul teoriilor gauge cu grupuri interne de simetrie.
Bibliografie
A. Lucrari proprii
în reviste indexate ISI
- G. Zet, V. Manta, C. Popa: Gauge Model Based on Group
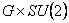 , Chin. Phys. Lett. Vol. 25 No.2 (2008) p. 433-435 (pdf) , Chin. Phys. Lett. Vol. 25 No.2 (2008) p. 433-435 (pdf)
- M. Chaichian, A. Tureanu, G. Zet: Corrections to Schwarzschild solution in non-commutative gauge theory of gravitation, Phys. Lett. B660 (2008) p. 573-578 (pdf)
în reviste indexate în baze de date internationale
- G. Zet: Unified Gauge Theory on Non-commutative space-time, Rom. J. Phys. Vol. 53 , No. 5-6 (2008) p. 635-644 (pdf)
- G. Zet, C. Popa: Spherical Gauge Gravitational Field and Spontaneous Symmetry Breaking , Rom. J. Phys. Vol. 53 , No. 5-6 (2008) p. 621-634 (pdf)
- G. Zet, C. Popa, D. Partenie: Gauge Symmetry of Gravitation, Bul. Inst. Politehnic Ia s i, Tom LIII ( LVII ), fasc. 1-2, Sectia Matematica. Mecanica Teoretica. Fizica (2007) p.103-114 (pdf)
- B. Ciobanu, I. Radinschi: Modeling the Electric and Magnetic Fields in Rotating Universe, Rom. J. Phys. Vol. 53 , No. 1-2 (2008) p. 405-416 (pdf)
- G. Zet, V. Manta : Gauge Theory with
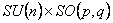 as structure group, Bul. Inst. Politehnic Iasi, acceptata pentru publicare 2008 (pdf) as structure group, Bul. Inst. Politehnic Iasi, acceptata pentru publicare 2008 (pdf)
prezentate la conferinte nationale si internationale
- G. Zet: General relativistic analog solutions for Yang-Mills theory on noncommutative space-time, Conferinta Nationala de Fizica Teoretica (CNFT3) 10-13 Iunie 2008, Busteni, Romania (pdf)
- G. Zet: U(2) gauge theory on non-commutativity geometry, Second Workshop on Quantum Gravity, 22-24 Septembrie 2008, Lusofona University, Lisbon
- V. Chiritoiu, G. Zet: Renormalization in Quantum Gauge Theory, Conferinta Nationala de Fizica, 10-13 Septembrie 2008, Bucuresti-Magurele
B. Lucrari ale altor autori
- M Blagojevic: Gravitation and Gauge Symmetry. IOP Publishing 2008
- N. Wu: Renormalizable Quantum Gauge Theory of Gravity, Commun. Theor. Phys. 38 (2002) p. 151-156
- N.Seiberg, E. Witten : String Theory and Noncommutativity Geometry JHEP 9909 (2008) 032
C. Lucrari proprii publicate anterior
- G. Zet, C.D. Oprisan, S. Babeti: Solutions without singularities in gauge theory of gravitation, Int. J. Mod. Phys. 15C (2004) p. 1031-1038
Sinteza etapei 2 in format PDF |